Large language models (LLMs) are increasingly being used as components within software systems. We live in a world where you can get computational fluid dynamics help from your friendly neighborhood Chevy care salesman chatbot. You can ask an LLM to perform automated literature reviews. You can even use them to simulate military strategy.
With the increasing zero-shot capabilities of frontier language models like GPT-4, Claude, and Gemini, we already see the proliferation of “LLM-powered” software systems. It feels like we will soon be able to build hyper-competent AI systems and agents just by prompting an extremely smart model!
On the other hand, LLMs are extremely hard to predict. Subtle shifts in prompting yield radically different performance (cf. Prompt Breeder, the GPT-3 paper, and How Can We Know What Language Models Know?). To make matters worse, Yann Lecun says that LLMs are “exponentially diverging stochastic processes”, which is rough for those of us hypothetically interested in buildng an AGI using LLMs.
I believe that control theory can help us make progress on the barriers separating us from being able to build hyper-competent LLM-based systems. Control-theoretic notions of reachability, controllability, and stability are readily applicable to LLM systems. Moreover, the lens of control theory naturally leads to a wide variety of tractable, fundamental problems to work on, using both empirical and analytic methods.
This post focuses on my motivations for pursuing LLM control theory. I hope you consider reading our paper “What’s the Magic Word? A Control Theory of LLM Prompting” for the details of our formalization and results on the controllability of LLMs.

Magic Words paper abstract -- available at arXiv:2310:04444
How do we currently understand LLM capability?
Studying and augmenting LLM capabilities currently revolves around zero-shot and few-shot benchmarks. To demonstrate the utility of a technique, LLM researchers often measure success on benchmarks like “HellaSwag”, “MMLU”, “TruthfulQA”, “MATH”, and other creatively named benchmarks. These benchmarks aim to measure how well an LLM is able to answer knowledge, reasoning, and mathematical questions. Benchmarks are a useful tool for understanding models, but they fail to account for the dynamical nature of LLM-based software systems. LLM system designers –a.k.a. prompt engineers– build software around an LLM to achieve some goal (e.g., teach students, sell cars, review job applications, perform research, etc.). The interaction between the software and the LLM yield non-trivial dynamics as the LLM generates text based on the current state (context), influencing the software, which in turn influences subsequent generation by modifying the LLM’s state.
Currently, LLM system design and prompt engineering is highly empirical. We lack guiding principles and theory on how these more dynamical LLM systems will act, particularly when we have partial control over the input (e.g., we directly control the system prompt) but incomplete control over some imposed tokens (e.g., user input or programmatic feedback from tools). Given a limited budget of controllable prompt tokens \(k\) and some imposed state tokens \(\mathbf x_0\), does exist a control input \(\mathbf u\) where \(|\mathbf u| \leq k\) that steers the model to produce some desired output \(\mathbf y\)? If not, is there some structure that determines which outputs are reachable? Can we find patterns in the controllability of language models from the perspective of zero-shot prompting? These are exactly the questions we seek to answer in our paper.
LLM Control Theory Overview
Thinking in the language of of control theory has brought me a lot of clarity in thinking about the questions that naturally arise in LLM systems development. Control theory studies how a “plant” system can be influenced toward a desired state using a “control signal” – often in the presence of disturbances and uncertainty. This is precisely our goal when building LLM-based systems. We have a strange, somewhat unpredictable system (LLM) for which we must build a programmatic controller that steers it toward achieving some objective, often in the presence of external disturbances (e.g., unpredictable user input). The system has an internal state, and is impinged upon by some external input (e.g., user input, programmatic tools like web browsers and terminals). The state is updated by sampling new tokens from the LLM or receiving external input tokens. Changes to the state affect future state updates, yielding non-trivial dynamics.
Control theory is usually taught in terms of continuous-time linear ordinary differential equations (ODEs). LLM systems, on the other hand, operate on variable length strings of discrete tokens, and are generally run in a stochastic manner. We highlighted the following differences between conventional ODE-based systems and LLM-based systems in our paper:
- Discrete state and time: LLM systems operate on sequences of discrete tokens over a discrete time set, in contrast to the continuous state spaces and time sets studied in classical control theory.
- Shift-and-Grow State Dynamics: Whereas the system state in an ODE-based system has a fixed size over time, the system state \(\mathbf x(t)\) for LLM systems grows as tokens are added to the state sequence.
- Mutual exclusion on control input token vs. generated token: The LLM system state \(\mathbf x(t)\) is written to one token at a time. The newest token is either drawn from the control input \(u(t)\) or is generated by the LLM by sampling \(x'\sim P_{LM}(x' | \mathbf x(t))\). This differs from traditional discrete stochastic systems, where the control sequence and internal dynamics generally affect the state synchronously.
Despite these differences, the mathematical machinery of control theory is still applicable. Our recent paper, What’s the Magic Word? A Control Theory of LLM Prompting develops control theory for LLMs, starting with the fundamental set-theoretic basis of mathematical systems and control theory. This lets us formalize notions of reachability, controllability, stability, and more for LLM-based systems. Importantly, our formalization is general enough to apply to LLM systems with a variety of augmentations, including tool-wielding, user interaction, and chain-of-thought style reasoning schemes.
Open Questions in LLM Control Theory
Developing methods to control a system is a great way to understand the system. Excitingly, the control theoretic lens immediately suggests a variety of tractable, fundamental questions about the nature of LLM systems. Here are a few exciting open questions we highlighted in the paper:
- Control Properties of Chain-of-Thought: Chain-of-Thought is a powerful technique where LLMs are allowed to generate intermediate tokens (i.e., “thoughts”) between a question and an answer. The control properties (e.g., stability, reachability) of systems leveraging these techniques are of great interest for understanding and composing systems of LLMs in the real world.
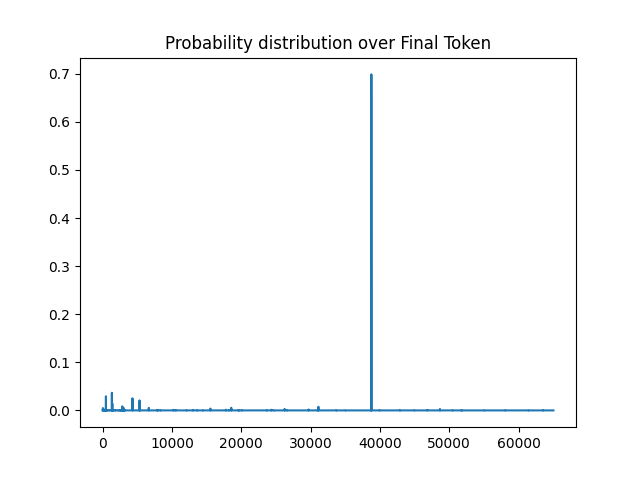
- Distributional Control: How precisely can we control the next-token distribution by manipulating the prompt? Can we force the KL-divergence between the next-token distribution and an arbitrary desired distribution to zero? While our work focuses on manipulating the probability distribution’s argmax (i.e., the most likely next token), it remains unclear how controllable the distribution is.
- Learnability of Control: To what extent can LLMs learn to control each other? The paper Large language models are human-level prompt engineers showed – you guessed it – that LLMs are capable of human-level prompt engineering, but it is unclear how well an LLM can learn to control another when explicitly optimized on the objective of LLM control.
- Controllable Subspaces: In the control of linear dynamical systems, it is known that uncontrollable systems are often coordinate transformable into a representation where a subset of the coordinates are controllable and a subset are uncontrollable. Our analytic results showed that controllable and uncontrollable components naturally emerge for self-attention heads. Can this be generalized to transformer blocks with nonlinearities and residual streams?
- Composable LLM Systems: One of the greatest boons of control theory is the ability to compose control modules and subsystems into an interpretable, predictable, and effective whole. The composition of LLM systems (potentially with non-LLM control modules) is an exciting avenue for scaling super intelligent systems.
Our Contributions to LLM Control Theory
In our paper, What’s the Magic Word? A Control Theory of LLM Prompting, we take the following steps toward establishing the discipline of LLM control theory:
- Formalize LLMs as a class of discrete stochastic dynamical systems.
- Investigate the reachable set of system outputs \(\mathcal R_y(\mathbf x_0)\), for which there exists a control input sequence \(\mathbf u\) for each \(\mathbf y \in \mathcal R_y(\mathbf x_0)\) that steers the LLM to output \(\mathbf y\) from initial state sequence \(\mathbf x_0\).
- Prove an upper bound on the controllability of token representations in self attention.
- Empirically study the controllability of a panel of open source language
models (Falcon-7b, Llama-7b, Falcon-40b) w.r.t. initial states sampled
from the Wikitext dataset, developing a tractable statistical metric
(“\(\pmb k-\pmb \epsilon\) controllability”) for measuring LLM
steerability.
- We find that the correct next Wikitext token following sequence \(\mathbf x_0\) is reachable over 97% of the time with prompts of \(k\leq 10\) tokens.
- We also establish that the top 75 most likely next tokens, as estimated by the LLM itself, are reachable at least 85% of the time with prompts of \(k\leq 10\) tokens.
- Short prompt sequences can dramatically alter the likelihood of specific outputs, even making the least likely tokens become the most likely ones.
I hope you consider reading the full paper and joining us in investigating LLMs through the lens of control theory!
]]>